Dimensional reduction of the 28 Spin(8) gauge bosons is motivated by the Lie group fibrations (where S6=G2/SU(3) and M8=G2/Spin(4)):
S3 -> S7 -> S4
Spin(7) -> Spin(8) -> S7
G2 -> Spin(7) -> S7
SU(3) -> G2 -> S6 S3 -> S7 -> S4
M8 -> G2 -> Spin(4)
along with Spin(4) -> Spin(5) -> S4 and S3 x S3 =Spin(4); S4=loc=U(1)4; S6 Spin(4); M8={7 quaternionic subalgebras of O, eH in O} SU(3).
From the fibrations, it appears that the 28-dimensional Lie group Spin(8) might be made up of 10-dimensional Spin(5), 8-dimensional SU(3), 6-dimensional Spin(4), and 4-dimensional S4.
However, even if S4 were the Lie group T4 = U(1)4, the Lie group Spin(8) is clearly not the Cartesian product Spin(5) x SU(3) x Spin(4) x T4.
Even if only the Lie algebra structure is considered, so that the Lie algebra of S4 = T4, the two fibrations of G2 cannot be done simultaneously because M8 SU(3) and M6 Spin(4).
Therefore, the Lie algebra Spin(8) is not given by the direct sum
Spin(5) = SU(3) = Spin(4) = T4 .
Spin(8) can be considered to be only a 28-dimensional vector space, and so decomposed into Spin(8) = R10 = R8 = R6 = R4.
Then a Lie algebra structure is introduced separately onto each factor of R10 = R8 = R6 = R4 in accordance with the Weyl symmetry of the Casimir operators of Spin(8).
The resulting reduction is Spin(8) -> Spin(5) x SU(3) x Spin(4) x U(1)4.
Since the F4 gauge boson dimensional reduction is not a trivial reduction of Spin(8) to a Cartesian product of subgroups, the Coleman-Mandula no-go theorem does not apply.
Before discussing the Weyl group structure, consider the Spin(8) Clifford algebra Cl(8) described in Appendix 1. Cl(8) has the same graded structure 1 + 8 + 28 + 56 + 70 + 56 + 28 + 8 +1 as the exterior algebra of forms. Both the scalar 0-form and the volume 8-form are in 1-dimensional graded spaces and have isotropy (or local symmetry) group Spin(8). Therefore, it is natural to construct the F4 model with an 8-dimensional (locally R8) spacetime base manifold and pure gauge structure related to the fibration Spin(8) -> Spin(9) -> S8.
In the F4 model, it is necessary to reduce the dimension of the spacetime base manifold from 8 to 4 in order to have a spacetime lattice (the D4 lattice) with nearest neighbor lightcone links.
Dimensional reduction of the spacetime base manifold is equivalent to choosing a p-form (p < 8 and p 0 for nontriviality) as the volume form of the p-dimensional reduced spacetime.
As discussed by Lawson and Michelsohn20 and by Harvey21, the only p-form (0 < p < 8) over R8 with isotropy group as large as Spin(7) is the Cayley 4-form F4 of the Cayley calibration. The Cayley 4-form F4 with Spin(7) isotropy group exists for all Riemannian 8-manifolds having Spin(7) holonomy. It is consistent with reduction to 4 dimensions.
Since the isotropy group of F4 is Spin(7) instead of Spin(8), Spin(8) cannot be the gauge group of the 4-dimensional F4 model.
Indeed, Spin(7) is also too big. To see this, use the following requirement of the F4 model:
The F4 model requires that the Laplacian of a gauge group G be realizable as the Laplace-Beltrami operator on a compact rank one Riemannian symmetric space G/K that can be mapped locally injectively into the spacetime base manifold.
The F4 model in 8 dimensions meets the requirement, because there is a compact rank one Riemannian symmetric space
Spin(8)/Spin(7) = S7 = O0 that is contained within the octonionic
8-dimensional spacetime. Therefore, the Spin(8) Laplacian is defined as the Laplace-Beltrami operator on the compact rank one Riemannian symmetric space S7 that is naturally contained within the octonionic 8-dimensional spacetime.
After reduction to 4 dimensions, the continuum spacetime base manifold is an approximation to the fundamental Planck-length D4 lattice spacetime.
Consider a Spin(7) gauge group and a 4-dimensional spacetime. Spin(7) has no compact rank one Riemannian symmetric with as few as 4 dimensions, since the symmetric spaces Spin(7)/Spin(6) = S6 and Spin(7)/G2 = S7 are more than 4-dimensional. (That they are the lowest dimensional compact rank one Riemannian symmetric spaces can be determined from tables such as those in Helgason12 or Besse22.)
Spin(6) in Spin(7) is too big, since the symmetric spaces
Spin(6)/Spin(5) = S5 and Spin(6)/S(U(3) x U(1)) = CP3 are more than 4-dimensional.
G2 in Spin(7) is too big, since the symmetric spaces G2/SU(3) = S6 and G2/Spin(4) = M8 are more than 4-dimensional.
Consider the F4 isotropy group Spin(7) as being fibred by
G2 -> Spin(7) -> S7.
G2 is fibred by SU(3) -> G2 -> S6 and Spin(4) -> G2 -> M8, and
S3 -> S7 -> S4.
The objective is to break up Spin(7) into G2 and S7, then break up G2 into SU(3) and Spin(4), then break up S7 into S3 = SU(2) and S4, and then identify S4 with the 4-torus T4. Clearly, such breaking up and identification cannot be done globally at the Lie group level because the fibrations are nontrivial and S4 is globally not T4. It cannot even be done as a local Lie algebra splitting, as the tangent space to S6 does not automatically have the Lie algebra structure of Spin(4) and the tangent space to M8 does not automatically have the Lie algebra structure of SU(3). It can be done at the level of tangent vector space structure, at which level
V{Spin(7)} = V{SU(3)} = V{SU(2)} = V{T4} = V{Spin(4)},
where V{G} denotes the vector space tangent to the Lie group G.
After Spin(7) is broken up into a sum of vector spaces S V{G},
the Lie group structure of G is reimposed on each element V{G} by using the Weyl group symmetry of Spin(8) … Spin(7).
The result is that the vector space sum
V{Spin(7)} = V{SU(3)} = V{SU(2)} = V{T4} 7=V{Spin(4)} becomes the Cartesian product SU(3) x SU(2) x T4 x Spin(4), which leads to the standard model SU(3) x SU(2) x U(1) x Lorentz. The S7 part of Spin(8) that is outside Spin(7) = Spin(8)/S7 can then be added on to give the Higgs mechanism from S3 = S7/S4 and translations from S4 = S7/S3.
SU(3) in G2 is consistent with the F4 model, since SU(3)/S(U(2) x U(1)) = = CP2, so that SU(3) is the color force gauge group.
SU(2) = S3 … S7 is all consistent with the F4 model, since SU(2)/U(1) =
= S2 in S2 x S2, so that SU(2) is the weak force gauge group.
T4 is consistent with the F4 model, since T4 = U(1)4 = S1 x S1 x S1 x S1, so that the 4 components of T4 are the x, y, z, and t covariant components of the electromagnetic photon.
Let Spin(4) be the Lorentz group. Consider S7 = Spin(8)/Spin(7), the 7 infinitesimal generators of Spin(8) being outside the F4 isotropy group Spin(7). Since S3 -> S7 -> S4, locally at the Lie algebra level the outside S4 is the 4-dimensional group of 4-dimensional spacetime translations. When combined with Spin(4), the outside S4 gives Spin(5) by the fibration Spin(4) -> Spin(5) -> S4. Spin(5) is all right, since Spin(5)/Spin(4) = S4. The outside S4 defines transport for the tangent space formulation of the F4 model quantum field theory.
The remaining outside S3 = SU(2) gives the Higgs scalar mechanism in a manner similar to that of Mayer23. It is related to the weak force SU(2) inside the Spin(7). Together, they are SU(2) x SU(2) = Spin(4), which is all right since [SU(2)/U(1)] x [SU(2)/U(1)] = S2 x S2.
The Lie group structure of the gauge group vector spaces in the F4 model dimensional reduction is based on reduction of the Weyl group S4 x Z23 of Spin(8) into the Weyl groups of SU(3), Spin(4), U(1)4, and Spin(5).
Consider polynomials on the Cartan subalgebra of Spin(8), and a set of coordinates {x,y,z,t}. As described by Zelobenko24, the algebra of all polynomials that are invariant under the Weyl group of Spin(8) can be identified with the algebra of all polynomials over the Lie algebra Spin(8) that are invariant under the adjoint representation of Spin(8), which can also be identified with the center of the universal enveloping algebra of the Lie algebra Spin(8). (The identifications are linear but not multiplicative.) Therefore, the elements of the algebra of all polynomials invariant under the Weyl group of Spin(8) are called the Casimir operators of Spin(8). Casimir operators are also described by Barut and Raczka25 and O'Raifeartaigh26. The Casimir operators of Spin(8) are generated by the following polynomials in {x,y,z,t}:
x2 + y2 + z2 + t2
x4 + y4 + z4 + t4
x6 + y6 + z6 + t6
xyzt .
The product of the degrees of the generating polynomials 2 x 4 x 6 x 4 = 192 is equal to the order of the Weyl group S4 x Z23 = 4 x 3 x 2 x 2 x 2 x 2 = 192.
Under F4 model dimensional reduction, the rank 4 Lie algebra Spin(8) is reduced into Lie algebras of rank no greater than 2. Rank 2 Lie algebras have only 2 generating Casimir operators, written as polynomials of 2
(or 3 in the case of unitary Lie algebras) variables.
Consider first the 2 lowest order Spin(8) Casimir operators,
x2 + y2 + z2 + t2 and x4 + y4 + z4 + t4 . They can be written in 2 variables as x2 + y2 and x4 + y4 , and are the Casimir operators for the rank 2 Lie algebra Spin(5) = Sp(2) with 10 infinitesimal generators. The Weyl group of Spin(5) = Sp(2) is S2 x Z22 of order 23 = 8 = 2 x 4.
Then consider the Spin(8) Casimir operator x6 + y6 + z6 + t6 .
It is of degree 6, and should correspond to a rank 2 Lie algebra whose Weyl group is of order 6. The Lie algebra must have a Casimir operator of degree 2 (the degree 2 Casimir operator defines the Laplace-Beltrami operator for the Lie algebra), so that the other generating Casimir operator must have degree 3 = 6/2. The only such Lie algebra is SU(3) with 8 infinitesimal generators. The SU(3) generating Casimir operators can be written (in 3 variables, as is convenient for unitary groups) as
x2 + y2 + z2 and x3 + y3 + z3. The Weyl group of SU(3) is S3 of order 3 x 2 = 6.
Now consider the last Spin(8) Casimir operator xyzt of degree 4. The only rank 2 Lie algebra whose Weyl group is of order 4 is
Spin(4) = Spin(3) x Spin(3) = SU(2) x SU(2) = Sp(1) x Sp(1) = S3 x S3 ,
with 6 infinitesimal generators and two degree 2 Casimir operators. In two variables, they can be written as x2 and y2 . The Weyl group of Spin(4) is S2 x Z2 of order 2 x 2 = 4.
The groups Spin(5), SU(3), and Spin(4) account for 10+8+6 = 24 of the 28 infinitesimal generators of Spin(8). The other 4 are the Cartan subalgebra of Spin(8), U(1)4 = S1 x S1 x S1 x S1 = T4 .
The Weyl group S4 x Z23 of Spin(8) is the semi-direct product of the Weyl groups S3, S2 x S2, I, and S2 x Z22
of SU(3), Spin(4), U(1)4, and Spin(5).
The semidirect product S3 x S2 x S2 x I x S2 x Z22 of the Weyl groups of SU(3), Spin(4), U(1)4, and Spin(5) is the unique semidirect product decomposition of the Weyl group of Spin(8), S4 x Z23, such that the identity component U(1)4 corresponds to the Cartan subalgebra of the rank 4 Lie algebra Spin(8) and the sum of the dimensions of Lie algebras of rank at most 2 equals 28, the dimension of Spin(8). For Lie algebras of rank at most 2, there is a 1-1 correspondence between the infinitesimal generators other than Cartan subalgebra elements, the root vectors, and the elements of the Weyl group reflections in root space hyperplanes perpendicular to the root vectors.
The decomposition into SU(4), U(1)4, and SU(2)3 = Spin(4) x SU(2) involves the rank 3 Lie algebra SU(4) = Spin(6), so the fibration Spin(6)=SU(4) -> Spin(7) -> S6 is not used.
Further, the fibration G2 -> Spin(7) -> S7 is consistent with the octonionic structure of the F4 model, while the fibration
Spin(6)=SU(4) -> Spin(7) -> S6 leads to
S3 -> S7 -> S4
Spin(7) -> Spin(8) -> S7
Spin(6)=SU(4) -> Spin(7) -> S6
S(U(3) x U(1)) -> SU(4) -> CP3
which is related to twistor theory, or
to
S3 -> S7 -> S4
Spin(7) -> Spin(8) -> S7
Spin(6)=SU(4) -> Spin(7) -> S6
Spin(5) -> Spin(6) -> S5 = SU(3)/S3
which gives the same structure as the G2 fibration if SU(3)/S3 is combined with S3 to give SU(3) and S6 is identified with Spin(4).
After dimensional reduction to 4-dimensional spacetime, the 28 infinitesimal generators of gauge group Spin(8) of the F4 model become the 8 generators of the color force SU(3), the 6 generators of the weak force-Higgs Spin(4) = SU(2) x SU(2), the 4 covariant (x,y,z,t) components of the electromagnetic U(1) photon, and the 10 generators of a Spin(5) gauge group that, by the MacDowell-Mansouri mechanism5,6,7, gives gravitation.
The Casimir operators of a Lie algebra not only can be characterized as the elements of the algebra of all polynomials over the Cartan subalgebra that are invariant under the Weyl group of the Lie algebra, or as the algebra of all polynomials over the Lie algebra that are invariant under the adjoint representation of any Lie group G with that Lie algebra, but also can be characterized as the differential operators on G = G/{e} (where e is the identity of G) that are bi-invariant under G (Helgason27, Ch.II, §4, No.2 ).
If K is a closed subgroup of G, let D(G/K) denote the algebra of differential operators on G/K that are left-invariant under G.
Note that, since the gauge group Lie algebras are taken to be complex semisimple Lie algebras such that gauge group propagators have a complex phase, the related polynomial algebras and differential operator algebras are complex algebras.
D(G/{e}) = D(G) is isomorphic to the universal enveloping algebra of the Lie algebra of G (Helgason12, Ch.II, §1, No.4) and there is a unique linear bijection l: S(g) -> D(G), where S(g) is the symmetric polynomial algebra over the Lie algebra g of G (Helgason27,Ch.II,§4,No.2).
l also identifies the set I(a) of Weyl-invariant polynomials in the symmetric polynomial algebra S(a) over a maximal Abelian subalgebra
a in g with set Dw(A) of Weyl-invariant differential operators over the maximal abelian subspace A in G (Helgason27, Ch.II, §5, No.2).
Let Z(G) denote the center of D(G) and I(g) in S(g) denote the set of polynomials over the Lie algebra g of G that are invariant under the adjoint representation of G. Then l(I(g)) = Z(G) and Z(G) is the set of right-invariant differential operators in D(G), or the bi-invariant differential operators on G (Helgason27, Ch.II, §4, No.2).
The generating Casimir operators of a gauge group G generate the algebra Z(G) of bi-invariant differential operators on G.
Z(G) always contains a quadratic generating Casimir operator, the Laplacian L(G) for the gauge group G.
For any compact rank one symmetric space G/K with Riemannian structure defined by the Killing form B(Xi,Xj) = gij of G, the Laplace- Beltrami operator L(G/K) on G/K generates the algebra D(G/K).
where Ls is the Laplace-Beltrami operator on the sphere S(r,p0) of radius r at point p‚ of G/K and A(r) is the area of S(r,p). Let V(r) be the volume of S(r,p), L be the diameter of G/K, and p° be antipodal to p0.
is the solution to Poisson's equation L(G/K) u(p) = ¶(p,p0) - ¶(p,p°) such that º u(q) dq = 0. The term - ¶(p,p°) is necessary because compactness of G/K requires that º [¶(p,p0) - ¶(p,p°)] dq = 0 for Poisson's equation to have a solution (Helgason27, Ch.II, §§4,5).
The solution g(p,p0) - g(p,p°) is the sum of Green's functions for the propagator at p0 of a gauge boson particle of gauge group G and the propagator at p° of a gauge boson antiparticle. Physically, the gauge boson antiparticle at p° is ignored and
is the Green's function for the propagator of the gauge bosons of the gauge group G. V(L) is the volume of G/K. The factor 1/V(L) normalizes the delta function ¶(p,p0) to 1.
The irreducible subgroups G of Spin(8) with compact rank one symmetric spaces G/K of dimension 4 or less are:
Spin(2) = U(1) = S1 (abelian) G/K = S1 = T1;
Spin(3) = SU(2) = Sp(1) = S3 G/K = S3 and G/K = S2 = SU(2)/U(1);
SU(3) G/K = SU(3)/S(U(2) x U(1)) = CP2; and
Spin(5) = Sp(2) G/K = Spin(5)/Spin(4) = S4.
Wolf28 has shown that T4, S2 x S2, CP2, and S4 are representatives of the four equivalence classes of complete simply connected Riemannian manifolds with quaternionic structure.
In the F4 model dimensional reduction, 4-dimensional spacetime may be compactified as T4, S2 x S2, CP2, S4, or as parallelizable RP1 x S3, whichever is convenient.
Note that there is no one basis for 28-dimensional Spin(8) with respect to which all 4-dimensional groups U(1)4, Spin(4), SU(3), and Spin(5) are simultaneously represented as subgroups of Spin(8).
To see explicitly how F4 dimensional reduction works, look at
the 52-dimensional Lie algebra F4 as being made up of the 28-dimensional adjoint bivector representation of Spin(8), the 8-dimensional vector representation of Spin(8), and the two 8-dimensional half-spinor representations of Spin(8).
Spin(8) is a 28-dimensional rank 4 Lie algebra 2 of whose 4 fundamental representations are the 8 and 28 dimensional graded vector and bivector spaces of the 16 x 16 Spin(8) Clifford algebra with graded dimensions 1 + 8 + 28 + 56 + 70 + 56 + 28 + 8 + 1 = 256 = 16 x 16.
The other two are 8-dimensional half-spinor representations that are the minimal ideals in the 16 x 16 Spin(8) Clifford algebra, so they come from the entire 1+8+28+56+70+56+28+8+1 = 256 dimensional graded space.
In the F4 model, the 8-dimensional vector representation V8 of Spin(8) is
taken to be the 8-dimensional spacetime (prior to dimensional reduction),
with basis {t, x, y, z, te, xe, ye, ze}. Due to octonionic structure, the basis is isomorphic to the octonions {1, i, j, k, e, ie, je, ke}.
In the F4 model, the two mirror image 8-dimensional half-spinor representations of Spin(8), S8+ and S8-, each having basis
{n, dr, dg, db, e, ur, ug, ub} also isomorphic to {1, i, j, k, e, ie, je, ke}, represent the first generation fermion particles and antiparticles.
The Spin(8) triality automorphisms V8 @ S8+ @ S8- can be represented by maps {X0, X1, X2, X3, Xe0, Xe1, Xe2, Xe3}
Xi : V8 {t, x, y, z,te, xe, ye, ze} -> S8± {n, dr, dg, db, e, ur, ug, ub}
X0 : t -> n ; .... ; Xe3 : ze -> ub .
The maps {X0, X1, X2, X3, Xe0, Xe1, Xe2, Xe3} form a basis for an 8-dimensional space that is isomorphic to V8 @ S8+ @ S8- .
In the following, the basis {X0, X1, X2, X3, Xe0, Xe1, Xe2, Xe3} is used to denote the bases of V8, and of S8+, and of S8-, all of which are isomorphic by Spin(8) triality. The 4-dimensional subspace spanned by {X0, X1, X2, X3} represents ordinary spacetime in V8, and the 4-dimensional subspace spanned by {Xe0, Xe1, Xe2, Xe3} represents the part of V8 that is reduced by dimensional reduction, called here the e-spacetime.
The 16 x 16 Spin(8) Clifford algebra has an 1+28+70+28+1=128- dimensional even subalgebra that is the two 8 x 8 diagonal submatrices.
The 1+28+35=64-dimensional upper 8 x 8 diagonal has the scalar, bivector, and self-dual 4-vector grades. It has 8-dimensional minimal left ideals that are internal symmetry half-spinors. The first minimal left ideal has 1 scalar {1} and 7 bivectors {X0 X1, X1 X2, X 2 X3, X3 Xe0, X 0 Xe1, X1 Xe2, X2 Xe3} .
The 7 bivector entries are the S7 in the fibration Spin(7) -> Spin(8) -> S7.
The other left ideals are bivectors, self-dual 4-vectors, or mixtures thereof.
Physically, interpret the minimal left ideal as fermion particles.
Then the scalar represents the Weyl fermion neutrino and the 7 bivectors represent the Dirac fermion electron and quark particles, with
basis {n, dr, dg, db, e, ur, ug, ub}.
It also has 8-dimensional minimal right ideals that are spacetime symmetry Dirac g half-spinors. The first minimal right ideal has 1 scalar, 3 bivectors, and 4 self-dual 4-vectors. The other right ideals are mixtures of bivectors and self-dual 4-vectors.
Let the first minimal right ideal determine the physical interpretation of the right minimal ideal as the spacetime Dirac g matrices. The scalar and the 3 bivectors represent the time and space gm of ordinary spacetime, and the self-dual 4-vectors represent the e-spacetime Dirac g matrices.
The 35+28+1=64-dimensional lower 8 x 8 diagonal has the anti-self-dual 4-vector, 6-vector (pseudo-bivector), and 8-vector (pseudoscalar) grades. It also has 8-dimensional minimal left ideals that are internal symmetry half-spinors and 8-dimensional minimal right ideals that are space-time symmetry (Dirac g) half-spinors.
The bivector adjoint representation of Spin(8) represents the 28 gauge bosons as the entries of an antisymmetric 8 x 8 matrix, with linearly independent upper triangular entries
0 X0X1 X0X2 X0X3 X0Xe0 X0Xe1 X0Xe2 X0Xe3
0 X1X2 X1X3 X1Xe0 X1Xe1 X1Xe2 X1Xe3
0 X2X3 X2Xe0 X2Xe1 X2Xe2 X2Xe3
0 X3Xe0 X3Xe1 X3Xe2 X3Xe3
0 Xe0Xe1 Xe0Xe2 Xe0Xe3
0 Xe1Xe2 Xe1Xe3
0 Xe2Xe3
0
Fig. 6
Prior to dimensional reduction of the 8-dimensional V8 spacetime, the F4 model Lagrangian action is
ºV8 [ -F8Ÿ*F8 + ¯S8± (g¶) S8± + gg + hÝ (dg/dA) ¶h ]
where V8 is an 8-dimensional spacetime,
F8 is an adjoint Spin(8) curvature 2-form, *F is the dual 6-form,
S8± is a spinor fermion field, g¶ is the Spin(8) Dirac operator,
gg is a gauge-fixing term, and hÝ (dg/dA) ¶h is a ghost term.
Dimensional reduction in the F4 model is accomplished by projecting the {te, xe, ye, ze } subspace of the 8-dimensional V8 into the {t, x, y, z} subspace. In the notation used here, the projection is Xei -> Xi .
After the dimensional reduction projection Xei -> Xi ,
the Spin(8) gauge group contains the product of the Spin(4) group of the weak force and the Higgs field, with 6 entries
0 Xe0Xe1 Xe0Xe2 Xe0Xe3
0 Xe1Xe2 Xe1Xe3
0 Xe2Xe3
0
Fig. 7a
and a Spin(4) subgroup of the Spin(5) group of MacDowell-Mansouri gravity, with 6 entries
0 X0X1 X0X2 X0X3
0 X1X2 X1X3
0 X2X3
0
Fig. 7b
The remaining 4 x 4 = 16 entries
X0Xe0 X0Xe1 X0Xe2 X0Xe3
X1Xe0 X1Xe1 X1Xe2 X1Xe3
X2Xe0 X2Xe1 X2Xe2 X2Xe3
X3Xe0 X3Xe1 X3Xe2 X3Xe3
Fig. 7c
do not make up a subgroup of Spin(8).
After the dimensional reduction projection Xei -> Xi , they might be considered to be a 4 x 4 matrix of 16 independent entries acting with respect to the surviving ordinary spacetime as a gauge group U(4), except for the restriction in the F4 model that gauge groups after dimensional reduction should have rank no greater than 2. (That is, that the rank 4 of the gauge group Spin(8) should also be reduced to no more than 4/2 = 2).
Therefore, in the F4 model the 4 entries
X0Xe0
X1Xe0
X2Xe0
X3Xe0
Fig. 7d
are treated as the "translation" S4 of the fibration Spin(4) -> Spin(5) -> S4
to produce the MacDowell-Mansouri gravity Spin(5) = Sp(2):
0 X0X1 X0X2 X0X3 X0Xe0
0 X1X2 X1X3 X1Xe0
0 X2X3 X2Xe0
0 X3Xe0
0
Fig. 7e
Of the remaining 12 entries, the 3 x 3 = 9 entries
X1Xe1 X1Xe2 X1Xe3
X2Xe1 X2Xe2 X2Xe3
X3Xe1 X3Xe2 X3Xe3
Fig. 7f
represent the U(3) subgroup of U(4). The U(3) includes an SU(3) gauge group for the color force and one of the 4 covariant components of the U(1) of electromagnetism.
The last remaining 3 entries
X0Xe1 X0Xe2 X0Xe3
Fig. 7g
represent the other 3 of the 4 covariant components of the U(1) of electromagnetism.
Attempts at simultaneous decomposition of Spin(8) are ineffective because Spin(8) is not the Cartesian product Spin(5) x Spin(4) x SU(3) x U(1) x U(1) x U(1) x U(1).
The physically realistic way to decompose the 28 infinitesimal generators
of Spin(8) after dimensional reduction from an 8-dimensional spacetime to a 4-dimensional spacetime is to group them according to
Weyl group symmetry into groups of 10, 6, 8, and 4 members.
Then the group of 10 becomes Spin(5) with base manifold S4,
the group of 6 becomes Spin(4) with base manifold S2 x S2,
the group of 8 becomes SU(3) with base manifold CP2, and
the group of 4 becomes U(1)4 with base manifold T4 = S1 x S1 x S1 x S1.
After dimensional reduction from an 8-dimensional base manifold to a 4-dimensional spacetime, the 28 infinitesimal generators of Spin(8) cannot act together as a globally transitive simple group on a 4-dimensional base manifold M4 to define a physical
gauge boson Lagrangian action as they did on the V8 base manifold of the
8-dimensional F4 model.
After dimensional reduction, the 28 infinitesimal generators of Spin(8) group themselves according to Weyl group symmetry into groups of 10, 6, 8, and 4 members. Each group must then be considered separately, as above. Then the group of 10 becomes Spin(5) with base manifold S4, the group of 6 becomes Spin(4) with base manifold S2 x S2, the group of 8 becomes SU(3) with base manifold CP2, and the group of 4 becomes U(1)4 with base manifold T4 = S1 x S1 x S1 x S1. The Weyl group of Spin(8) is the semidirect product of the Weyl groups of the groups into which Spin(8) is reduced:
S4 x Z2£ = I4 x S2 x Z22 x S3 x S2 x S2 .
The Weyl group of a rank n Lie algebra can be represented as the finite group of reflections in Rn through hyperplanes through the origin perpendicular to vectors from the origin called root vectors. The root vectors can be represented by points in Rn. Weyl chambers for a Lie algebra are defined as the connected components of Rn into which it is divided by all the hyperplanes of fixed points of all the root vectors. The Weyl group is the group of reflections that permute the Weyl chambers in a simply transitive way (see Bröcker and tom Dieck8). For Spin(8), there are 12 Weyl hyperplanes and 192 Weyl chambers. There are 8 Weyl chambers for each of the 24 octahedral faces of the 24-cell.
The 24 octahedral faces are 4 loops of 6 octahedral faces each (see Coxeter18). To go from any Weyl chamber to another, first go to the proper one of the 4 loops (using the symmetry of the Weyl group of SU(2) x SU(2) = Spin(4)), then go to the proper octahedral face of the 6 within the loop (using the symmetry of the Weyl group of SU(3)), and finally go to the proper Weyl chamber of the 8 within the octahedral face (using the symmetry of the Weyl group of Spin(5)).
The 48 root vector vertices of the F4 Lie algebra, make up a 24-cell
{±1, ±i, ±j, ±k, (±1±i±j±k)/2} and
the dual 24-cell {(±1±i), (±1±j), (±1±k), (±i±j), (±i±k), (±j±k)} .
The 24 root vectors (±1±i), (±1±j), (±1±k), (±i±j), (±i±k), and (±j±k) correspond to 24 of the 28 infinitesimal generators of Spin(8).
The 4 infinitesimal generators of the Cartan subalgebra of Spin(8) are identified with the photon of the electromagnetic force.
The 24 infinitesimal Lie algebra generators corresponding to the root vectors of Spin(8) are identified by first projecting the Spin(8) root vector 24-cell into the 2-dimensional subspace spanned by {j,k}, which is the subspace perpendicular to the lines {±1} and {±i}.
Then {(-1±i), (-1±j), (-1±k)} is projected onto
{0, 0, +j, -j, +k, -k}, the root vector space of Spin(4)= SU(2) x SU(2).
The set {(+1±i), (+1±j), (+1±k), (±j±k)} is projected onto
{0, 0, +j, -j, +k, -k, (±j±k)}, the root vector space of Spin(5)=Sp(2).
For the remaining root vector set {(±i±j), (±i±k)}, right-multiply by (+1+i) to get (up to scale) {(+1-i±j±k), (-1+i±j±k)}. Project by {±1} -> 0 to get the 3-cube {±i±j±k}. Project by {±(+i+j+k)} -> 0 to get the hexagonal root vector space of SU(3) as the projection of the other corners {(+i+j-k), (-i-j+k), (+i-j+k), (-i+j-k), (-i+j+k), (+i-j-k)} .
A 2-dimensional projection of the 4-dimensional 24-cell is shown
in Fig. 8:
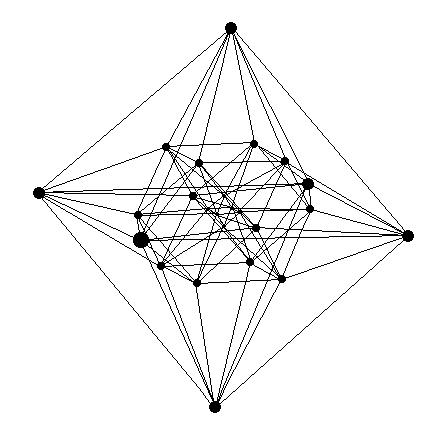
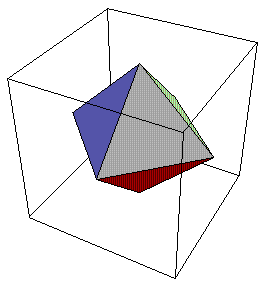
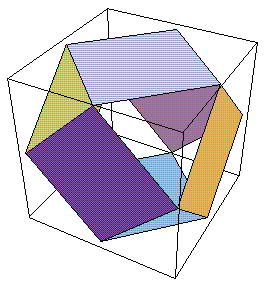
The geometric structure of the 24-cell shown in Fig. 8 is that of an outer octahedron, surrounding a middle cuboctahedron, in turn surrounding an inner octahedron. This can be drawn in Mathematica as in the following Notebook:


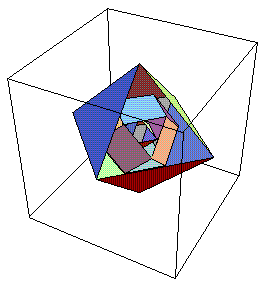

Relation of Gauge Bosons to Fermions and 8-dim Spacetime:
Of the 48 root vector vertices of the F4 Lie algebra, 24 vertices
{±1, ±i, ±j, ±k, (±1±i±j±k)/2} can be related to the other 24 vertices {(±1±i), (±1±j), (±1±k), (±i±j), (±i±k), (±j±k)} by quaternionic right-multiplication (up to scale factors of Ã2) by (+1+i), which takes
1 -> (+1+i), i -> (-1+i), j -> (+j+k), and k -> (-j+k).
That gives the following relationship between gauge bosons, fermions, and 8-dimensional spacetime (ignoring scale factors of 2): Spin(5): {(+1±i), (+1±j), (+1±k), (±j±k)} goes to {+2, +2i, (+1+i±j±k), ±2j, ±2k}.
The Spin(5) Cartan subalgebra goes to the {+2, +2i} of time and one space dimension. The {±2j, ±2k} has the other two space dimensions.
The {(+1+i±j±k)} contains 1 lepton-type and 3 quark-type fermions.
Spin(4): {(-1±i), (-1±j), (-1±k)} goes to {-2, -2i, (-1-i±j±k)}.
The Spin(4) Cartan subalgebra goes to the {-2, -2i} of time and one space dimension.
The {(-1-i±j±k)} contains 1 lepton-type and 3 quark-type fermions.
SU(3): {(±i±j), (±i±k)} goes to {(+1-i±j±k), (-1+i±j±k)} of
2 lepton-type and 6 quark-type fermions.
The SU(3) Cartan subalgebra goes to {(-1+i+j+k), +1-i-j-k)}, related to the 2 lepton-type fermions.
The photons in 8 dimensions correspond to the Cartan subalgebra U(1)4 of Spin(8). Therefore the action of photons on elementary fermions is described by the identity automorphism. Photons do not change the nature of elementary fermions, or, to put it another way, photons do not carry either electric or color charge.
The groups Spin(5), SU(3), SU(2), and U(1) are all or rank 2 or less so there is a 1-1 correspondence between their Weyl group elements and their root vectors, unlike the unreduced Spin(8) group that has 24 root vectors and a Weyl group with 192 elements.
The root vector diagrams of Spin(5), SU(3), Spin(4) = SU(2) x SU(2), and U(1)4 are shown in Fig. 9:
* * * * * * * * 2 * * 2 * 1 1 1111 * * * * * * * Spin(5) SU(3) Spin(4) U(1)4
The following figures summarize the action of charged gauge bosons on the elementary fermion particles of the first generation:
Weak Bosons:
W+: {e, ie, je, ke} ---> {1, i, j, k}
W-: {1, i, j, k} ---> {e, ie, je, ke}
Gluons:
gl-1: {i, ie} ---> {j, je}
gl-2: {i, ie} ---> {k, ke}
gl-3: {j, je} ---> {k, ke}
gl-4: {j, je} ---> {i, ie}
gl-5: {k, ke} ---> {i, ie}
gl-6: {k, ke} ---> {j, je}
Gravitons:
gr-1: {1, i, j, k} ---> {e, ie, je, ke}
gr-2: {e, ie, je, ke} ---> {1, i, j, k}
gr-3: {1, i, j, k} ---> {ke, je, ie, e}
gr-4: {ke, je, ie, e} ---> {1, i, j, k}
gr-5: {1, i, j, k} ---> {je, ke, e, ie}
gr-6: {je, ke, e, ie} ---> {1, i, j, k}
gr-7: {1, i, j, k} ---> {ie, e, ke, je}
gr-8: {ie, e, ke, je} ---> {1, i, j, k}.